Ученые разработали гибридный эволюционный алгоритм, который позволяет оптимизировать пропускную способность городских дорог на 5–15%. Система сочетает в себе методы агентного имитационного моделирования, искусственный интеллект и некоторые математические и биологические (эволюционные) принципы, благодаря чему, анализируя тысячи возможных конфигураций дорог, находит самые эффективные варианты расположения дорожной инфраструктуры. Разработка будет полезна при проектировании более удобных и менее загруженных дорожных сетей, включая многоуровневые развязки и тоннели. Результаты исследования, поддержанного грантом Российского научного фонда, опубликованы в журнале IEEE Access.
Современные города, особенно мегаполисы, сталкиваются с растущими транспортными проблемами — пробками и неэффективным использованием дорожного пространства. Традиционные методы проектирования дорожных сетей — математические модели, статический анализ пропускной способности и ручное проектирование — часто не учитывают динамику транспортных потоков и сложность городской инфраструктуры.
Использовать алгоритмы на основе искусственного интеллекта в этом случае эффективнее. Они могут предложить более адаптивные решения, поскольку способны анализировать большое количество различных транспортных потоков в реальном времени. Однако большинство существующих решений фокусируются на узких задачах: одни алгоритмы оптимизируют только светофорное регулирование, другие работают исключительно с поиском кратчайших маршрутов, третьи моделируют потоки на отдельных перекрестках без учета общей сетевой структуры. Поэтому нужны новые инструменты, которые будут одновременно анализировать и оптимизировать все ключевые параметры дорожной сети.
Ученые из Центрального экономико-математического института РАН (Москва) разработали гибридный генетический алгоритм, который сочетает методы многоагентного моделирования, искусственного интеллекта, теорию графов — математические инструменты, описывающие свойства сетей и связей между их элементами, — и эволюционные принципы изменчивости живых организмов. Система ищет оптимальные решения посредством механизмов, аналогичных тем, что существуют в биологии, — отбору, кроссинговеру (обмену участками хромосом при делении клеток) и мутациям. Используя предложенный алгоритм нечеткой кластеризации, система анализирует структуру транспортного потока, предсказывает заторы и предлагает оптимальную конфигурацию новых дорог, включая расположение перекрестков, эстакад и туннелей.
Для тестирования системы исследователи создали серию моделей различной сложности, в частности микроскопические, основанные на отдельных агентах — транспортных средствах, и мезоскопические, оперирующие агентными кластерами (группами транспортных средств). Эти модели разработаны на основе феноменологического подхода Бекларяна — Акопова, который авторы ранее успешно применили для анализа дорожного движения в сетях типа «Манхэттенская решетка».
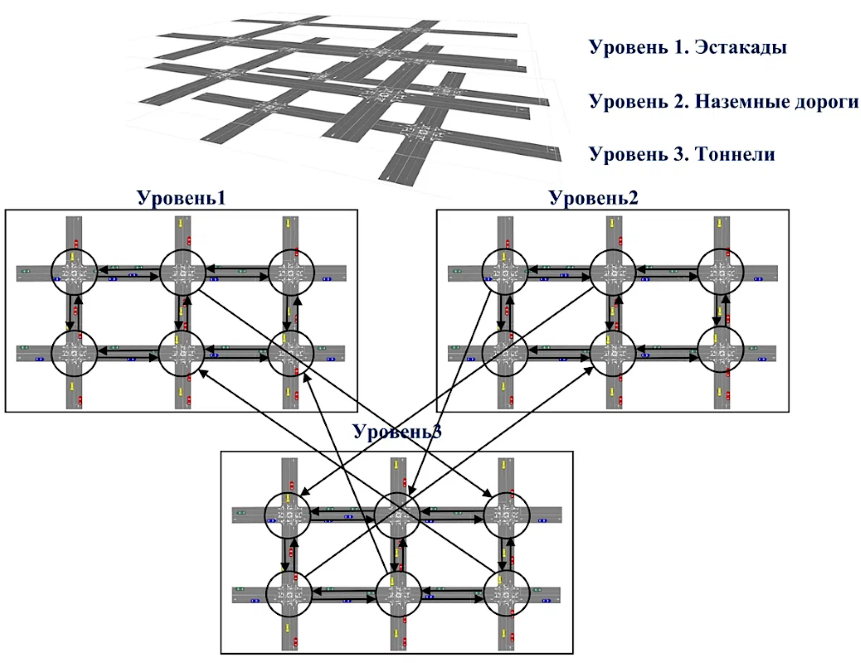
Модели используют системы дифференциальных и конечно-разностных уравнений для моделирования различных сценариев движения и взаимодействия транспортных средств. Простейшие из них были сопоставимы по масштабу с обычным перекрестком и использовались для отработки базовых функций разработанного оптимизационного алгоритма. Более сложные модели, напоминающие современные трехуровневые транспортные развязки с тоннелями и многоуровневыми съездами, позволили проверить алгоритм в условиях, приближенных к реальному городу. Кроме того, авторы смоделировали различные сценарии транспортной нагрузки — от обычного движения до экстремально высокой загруженности.
Эксперименты показали, что система позволяет эффективно улучшать пропускную способность транспортной сети. Так, например, согласно моделированию, повысить скорость потока транспортных средств на 5–15% можно, лишь немного увеличив количество дорожных развязок в городе — приблизительно на 1–5% от общей длины дорог.
«Наш алгоритм позволяет проектировать многоуровневые и многосвязные дорожные сети, способные эффективно функционировать даже в условиях высокой нагрузки. В будущем такие решения помогут городам уменьшить пробки и сделать передвижение по автодорогам комфортнее. В дальнейшем мы планируем искать способы оптимизации для более сложных дорожных развязок и участков дорог, таких как кольцевые и спиральные развязки. Эти элементы дорожных сетей будут также включать разнообразные составляющие транспортной инфраструктуры, такие как "умные светофоры", многоуровневые парковки и инфраструктуру для беспилотного транспорта», — рассказывает участник проекта, поддержанного грантом РНФ, профессор РАН Андраник Акопов, доктор технических наук, кандидат экономических наук, главный научный сотрудник лаборатории динамических моделей экономики и оптимизации Центрального экономико-математического института РАН.
Подписывайтесь на InScience.News в социальных сетях: ВКонтакте, Telegram, Одноклассники.





